⏳복잡도

자료 구조(data structure)는 데이터를 효율적으로 관리하고, 빠르게 수정·삭제·탐색·저장할 수 있도록 구성한 구조적 집합을 말합니다.

⏱️ 시간 복잡도

시간 복잡도란 ‘입력 크기(n)에 따라 알고리즘이 실행되는 데 필요한 시간 증가량’을 분석하는 척도입니다.

🧮 빅오 표기법

주요 로직의 반복 횟수를 기준으로 알고리즘의 성능을 표현하며, 이를 빅오(Big-O) 표기법으로 나타냅니다.
예를 들어, 입력 크기 n에 대한 알고리즘 수행 시간이 10n² + n이라고 하면 다음과 같은 반복문 구조를 상상할 수 있습니다.

for(int i=0;i<10;i++){
    for(int j=0;j<n;j++){
        for(int k=0;k<n;k++){
            if(true) cout<<k<<'\n';
        }
    }
}

for (int i=0;i<n;i++){
    if(true) cout<<i<<'\n';
}

빅오 표기법은 입력 크기(n)가 커질 때 가장 크게 영향을 미치는 항만 남기고 나머지는 제거하는 방식입니다.
위 알고리즘의 경우 n² 항이 지배적이므로 시간 복잡도는 O(n²)이 됩니다.

이유는 단순합니다. 입력이 커질수록 n² 성장이 다른 항들(n, 상수항)에 비해 압도적으로 크기 때문에, 속도 차이를 결정하는 본질적인 성능만 보겠다는 관점이 바로 빅오 표기법입니다.

⚡ 시간 복잡도의 존재 이유

시간 복잡도는 더 효율적인 코드로 개선할 수 있는 기준이 됩니다. 예를 들어, 버튼 클릭 후 화면이 나타나는 시간이 O(n²) 알고리즘 때문에 9초라면, 동일 기능을 O(n) 알고리즘으로 개선하면 3초로 단축될 수 있습니다. 즉, 시간 복잡도는 성능을 정량적으로 비교하게 해주는 매우 중요한 기준입니다.

📈 시간 복잡도의 속도 비교

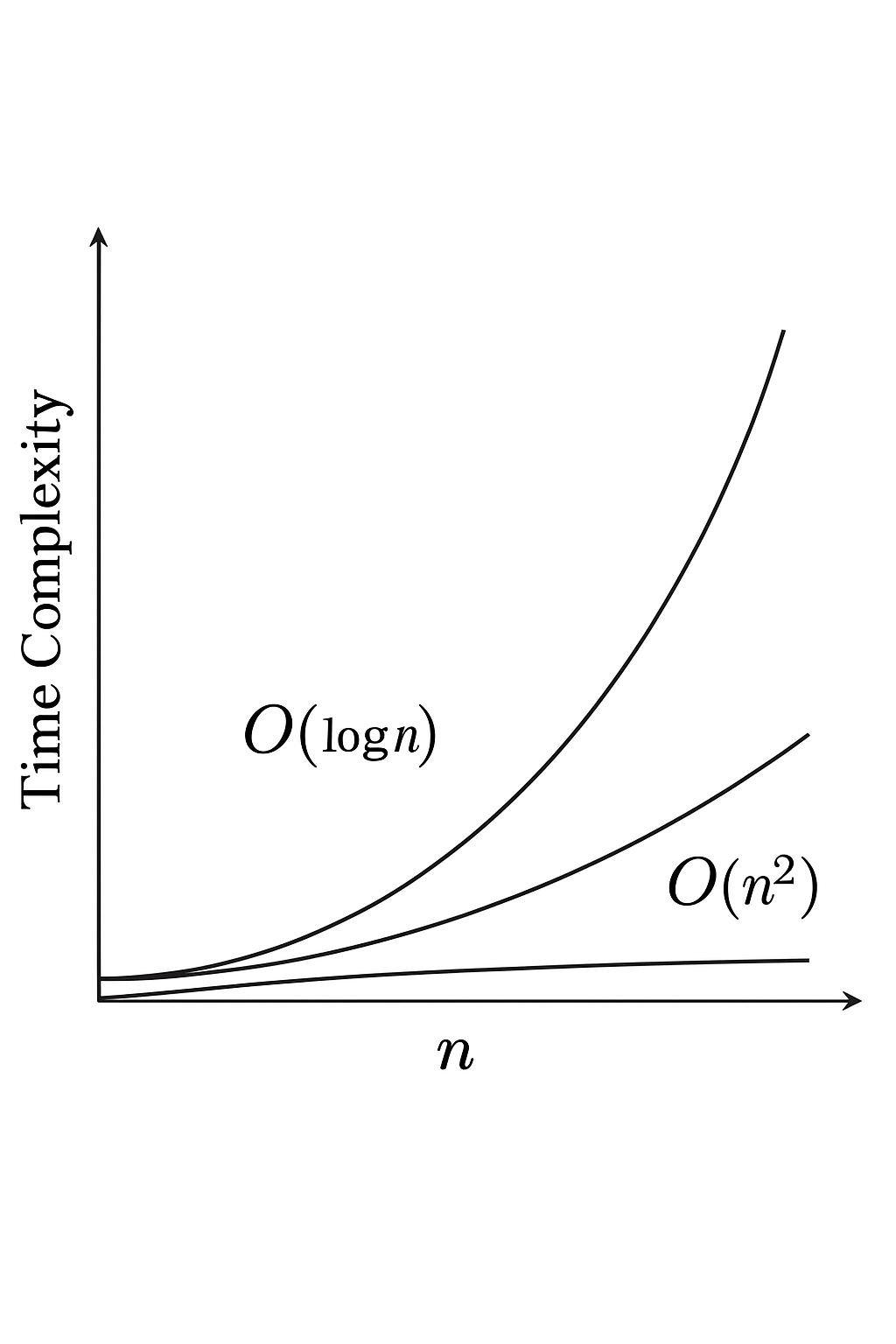
O(1)과 O(n)은 입력 크기가 커질수록 속도 차이가 급격히 벌어지는 것을 볼 수 있습니다. 또한 O(n²) 은 O(n)보다 훨씬 느려지고, 가능하다면 더 낮은 복잡도를 지향해야 합니다.

---

💾 공간 복잡도

공간 복잡도는 프로그램이 실행될 때 필요한 메모리 공간의 양입니다. 정적 배열뿐만 아니라 재귀 호출로 인해 추가적으로 필요한 스택 메모리 등도 모두 포함됩니다.

int a[1004];

위 코드처럼 정적 배열을 선언하면, a 배열은 1004 × 4바이트의 메모리 공간을 차지하게 됩니다. 이러한 공간 사용량 전부가 공간 복잡도에 포함됩니다.

---

🗂️ 자료 구조에서의 시간 복잡도

자료 구조를 선택할 때는 해당 구조의 접근·탐색·삽입·삭제가 각각 어떤 시간 복잡도를 가지는지를 반드시 고려해야 합니다.특히 평균 시간 복잡도와 최악(worst-case) 시간 복잡도를 함께 보는 것이 중요합니다.

🔄 자료 구조의 평균 시간 복잡도

자료 구조	접근	탐색	삽입	삭제
배열(array)	O(1)	O(n)	O(n)	O(n)
스택(stack)	O(n)	O(n)	O(1)	O(1)
큐(queue)	O(n)	O(n)	O(1)	O(1)
이중 연결 리스트(doubly linked list)	O(n)	O(n)	O(1)	O(1)
해시 테이블(hash table)	O(1)	O(1)	O(1)	O(1)
이진 탐색 트리(BST)	O(longn)	O(logn)	O(logn)	O(logn)
AVL 트리	O(logn)	O(logn)	O(logn)	O(logn)
레드 블랙 트리	O(logn)	O(logn)	O(logn)	O(logn)

📉 자료 구조 최악의 시간 복잡도

자료 구조	접근	탐색	삽입	삭제
배열(array)	O(1)	O(n)	O(n)	O(n)
스택(stack)	O(n)	O(n)	O(1)	O(1)
큐(queue)	O(n)	O(n)	O(1)	O(1)
이중 연결 리스트(doubly linked list)	O(n)	O(n)	O(1)	O(1)
해시 테이블(hash table)	O(n)	O(n)	O(n)	O(n)
이진 탐색 트리(BST)	O(n)	O(n)	O(n)	O(n)
AVL 트리	O(logn)	O(logn)	O(logn)	O(logn)
레드 블랙 트리	O(logn)	O(logn)	O(logn)	O(logn)

---

1. 자주 사용하거나 알고 있는 정렬 알고리즘(e.g., 퀵 정렬, 병합 정렬) 중 하나를 설명하고 시간 복잡도를 말해주세요.

퀵 정렬은 기준이 되는 피벗을 하나 선택한 뒤, 이를 기준으로 작은 값과 큰 값으로 분할하면서 정렬하는 알고리즘입니다. 평균적으로 분할이 균형 있게 이루어질 경우 시간 복잡도는 O(n log n)이며, 피벗이 한쪽으로 치우치게 선택되면 최악의 경우 O(n²)의 시간 복잡도를 가집니다.